Multiple scattering of sound in a school of fish produces complex spatial distributions of the acoustic (pressure) field p(r, t) and its intensity I(r,t). The random distributions of the pressure field and the intensity called "speckles" (Fig. 2) are analogous to optical speckles observed in laser beam scattering by a colloid.

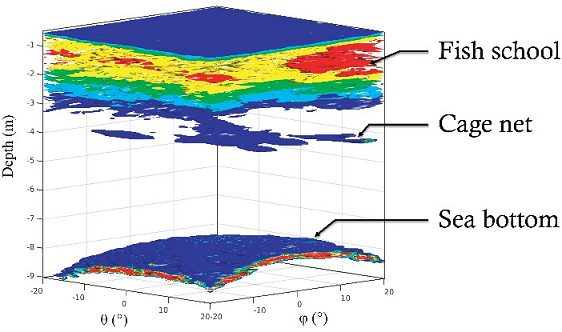
Figure 2. Three-dimensional ultrasound intensity speckle measured for sound scattering by a school of fish.

The speckles are characterized by the statistical distributions of p and I as well as by their spatial and temporal correlations (Fig. 3).

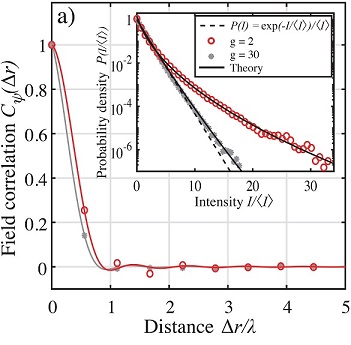
Figure 3. The correlation of the acoustic field backscattered by a dense school of fish. The red and gray curves correspond to the dense and sparse schools, respectively. The inset shows the statistical distribution of the scattered intensity P(I).

Our preliminary measurements show that for dense schools of fish, P(I) deviates from a simple exponential law expected in the weak scattering regime (the inset of Fig. 3) while the spatial correlation of intensity can be long range or even infinite. This experimental observation motivates the first problem to be solved in this project: to develop a theoretical model for the spatial and temporal correlations of the scattered sound from a dense school of fish. The temporal correlation can also be calculated from the experimental data and its decay with time can give us information about the movement of the fish in the cage under the condition of having a theoretical model adapted for its interpretation.

To perform this task, we will use the theoretical methods developed for electrons and photons in disordered media. An adaptation of these methods to the case of scattered sound from schools of fish will be necessary to take into account
(1) the complex structure of a fish: a strong scatterer (swim bladder) surrounded by soft tissues;
(2) the geometry of the experiment: a source and a detector in the shape of a cross on the surface of a semi-infinite medium;
(3) the collective motion of the fish which is different from the Brownian motion of small particles in suspension and affects the decorrelation of the field over time.

The expected results of this task include theoretical expressions for the correlation functions for the pressure field and its intensity as a function of separation in space and time delay. These expressions will be applied to describe the experimental data and characterize sound scattering by dense schools of fish (determination of ℓ by theoretical fitting) as well as the collective dynamics of fish ("scattering wave spectroscopy").